 |
|
| Informatik Abt. I | Diplomarbeiten im Bereich Algorithmische Geometrie |
|
|
|
| Informatik Abt. I | Diplomarbeiten im Bereich Algorithmische Geometrie |
Gegeben ist eine polygonale Kette C, die keine Selbstschnitte aufweist.
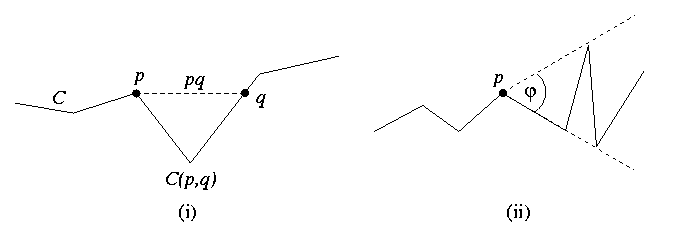
Der maximale Umweg von C ist definiert als:
Umweg(C) := maxp,q ( |C(p,q)| / |pq| ),wobei |C(p,q)| die Länge des Weges von p nach q auf C angibt, vgl. Abb. (i). Es soll ein Java Applet erstellt werden, daß (u.a.):
Den maximalen Umweg berechnet, hierfür ist ein effizienter Algorithmus bekannt.
Den kleinsten Winkel phi berechnet, so daß für jeden Punkt p auf der Kette C der Rest der Kette in einen Winkel der Größe phi paßt, Abb. (ii)
Oswin Aichholzer, Franz Aurenhammer, Christian Icking, Rolf Klein,
Elmar Langetepe, Günter Rote
phi-Self-Approaching Curves
Technical Report 226, Department of Computer Science, FernUniversität Hagen, Germany, 1997.
Annette Ebbers-Baumann, Rolf Klein, Elmar Langetepe, Andrzej Lingas.
A fast algorithm for approximating the detour of a polygonal chain.
In Algorithms - ESA '01, Lecture Notes Comput. Sci. Springer-Verlag, 2001.
Manuel Abellanas, Ferran Hurtado, Christian Icking, Rolf Klein,
Elmar Langetepe, Lihong Ma, Belén Palop, Vera Sacristán
[ Geometrie Labor ]
© Universität Bonn, Informatik Abt. I - webmaster - Letzte Änderung: Wed Jul 16 14:12:07 2008
Smallest color-spanning objects
Zu Erstellen ist ein Java-Applet für folgendes Problem:
Gegegen ist eine Menge von Punkten in der Ebene mit unterschiedlicher Farbe.
Finde ein kleinstes, achsenparalleles Rechteck (Quadrat in beliebiger
Orientierung, Kreis etc.), das von jeder Farbe mindestens einen Punkt
enthält.
Literatur
Smallest Color-Spanning Objects
Technical Report 283, Department of Computer Science, FernUniversität Hagen, Germany, 2001.
[ Informatik Abt. I ]
[ Forschung ]
[ Lehre ]
[ Publikationen ]
[ Mitarbeiter ]
[ Universität Bonn ]